Die Collatz-Vermutung
8. Januar 2011
Per Zufall bin ich auf ein interessantes, ungelöstes mathematisches Problem gestossen.
Ob Samuel dieses Problem gekannt hat - er hätte sicherlich seine Freude daran
Dieses Collatz-Problem, auch als (3n + 1)-Vermutung bezeichnet, ist ein ungelöstes mathematisches Problem, das 1937 von Lothar Collatz entdeckt wurde.
Bei dem Problem geht es um Zahlenfolgen, die nach einem einfachen Bildungsgesetz konstruiert werden:
Beginne mit irgendeiner natürlichen Zahl N > 0.
Ist N gerade, so nimm als nächstes N/2,
ist N ungerade, so nimm als nächstes 3N + 1.
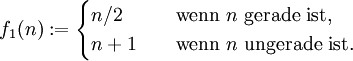
Die Summe der Buchstabenwerte von SAMUEL ist 19+1+13+21+5+12=71
Für 71 ergibt sich die Reihe
71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1
Diese hat 103 Elemente
Anscheinend mündet jede Folge in den Zyklus 4, 2, 1 – egal welche Startzahl man probiert hat.
Die Collatz-Vermutung lautet: Jede so konstruierte Zahlenfolge endet im Zyklus 4, 2, 1, egal, mit welcher natürlichen Zahl man beginnt.
Es wird intensiv nach Anfangswerten gesucht, die eine grosse Anzahl Elemete liefern, zur Zeit ist der Rekord bei
N = 274133054632352106267
hier der link zur Rekord-Seite
PS: natürlich liefert trivialerweise die Zahl N=2n eine Reihe mit n+1 Elementen. Gesucht sind aber möglichst "kleine" Ausgangswerte mit möglichst vielen Elementen.
Auf der Homepage von Jürgen Dankert, Professor für Informatik an der HAW Hamburg habe ich ein Script entdeckt, das ich etwas angepasst hier gerne wiedergeben möchte.
Man kann beliebig grosse Zahlen eingeben (wie etwa die oben angezeigte Rekord-Zahl).
Erzeugen einer Collatz-Folge
Bitte Anfangswert (positive ganze Zahl) eingeben, danach OK anklicken: